어드밴티지와 피드백 루프

들어가며

 

    최근 4학년 1학기로 학교 생활이 시작됐다. 이전 학기인 3학년 2학기에는 수학이 활용되는 강의에 스트레스받기 싫어서 관련 강의를 피했는데, 이번 학기에는 졸업을 위해 어쩔 수 없이 '디지털 통신 시스템'이라는 수학을 활용하는 강의를 듣게 됐다.

 

    휴학 기간까지 포함해 약 2년 만에 접하는 수학이어서 걱정이 많았다. 하지만, 이런 걱정과는 다르게 강의는 재미있었다. 수식에 의미를 담아 목표로 진행하는 과정이 이상하게도 재미를 느끼는 과정과 유사해 보였다.

 

    이전까지는 수식 자체에 어떤 의미가 있는 줄 알고 수식의 의미에 대해 집중했는데, 이제 와서 생각해 보면 수식 자체가 의미를 갖는 것이 아닌 그저 어떠한 현상에 대한 상징을 재해석하여 이해하기 쉽거나 다른 수식과 결합되기 쉽도록 변환하는 과정, 즉 흐름이라는 생각을 했다.

 

    재미 또한 마찬가지다. 내가 이전의 Lost In Hope 회고록 (3)에서 언급한 것처럼 재미는 시스템 그 자체에 의미가 있기보다는 시스템과 시스템 사이의 관계와 그 관계의 흐름에 의해 만들어진다고 생각한 점에 있어서 수식 계산 과정과 비슷해 보였다.

 

    재미 또한 시스템에 의해 특정 재미에서 다른 재미로 변환되고, 연결되며, 하나의 경험이 만들어지니 말이다.

 

 

    잡설이 길었다. 그냥 나는 이런 연유로 '수학에 다시 관심을 가지고 조금씩 무언가를 하고 있다.'정도로 이해하면 좋을 것 같다. 그리고, 오늘은 '이런 무언가'의 일환으로 최근에 읽고 있는 <Game Mechanics>라는 책의 내용을 테스트하고 정리하여 실제로 활용할 수 있게 체화해보고자 한다.

 

    오늘 다룰 내용은 어드밴티지와 피드백 루프가 게임에 어떤 영향을 미치는지에 대한 내용인데, 그냥 책에 있는 예제를 실습해 보고 이를 파이썬으로 구현해 보면서 내 예상과 실제 결과에 대한 비교를 통해 괴리를 줄이는 과정을 정리할 예정이다.

    

 

 

목차

1. 양성 순환 구조와 부정 회귀 구조형 농구
2. Machinations.io를 활용한 모델링
3. Python으로 변환 및 시각화
4. 가설과 검증
5. 결론

 

 

 

어드밴티지와 피드백 루프

---

양성 순환 구조와 부정 회귀 구조형 농구

 

    책에서는 피드백 루프에 대한 소개를 하며 '양성 순환 구조와 부정 회귀 구조형 농구'라는 예시를 제시한다. 게임의 전제는 다음과 같다.

 

1. 각 팀은 5명의 팀원으로 시작한다.
2. 팀원은 step 별로 확률에 따라 1점을 획득할 수 있다.
3. A 팀의 팀원은 40% 확률로 득점한다.
4. B 팀의 팀원은 20% 확률로 득점한다.
5. 점수 차이가 5점이 벌어질 때마다 선수가 1명씩 투입된다.
6. 양성 순환 구조형 농구에서는 우세한 팀에 선수가 투입된다.
7. 부정 회귀 구조형 농구에서는 열세한 팀에 선수가 투입된다.

 

    이 규칙에 따른 결과를 한번 생각해 보자. 1번부터 4번 규칙만 생각하면 A팀은 B팀보다 실력이 좋기에 그냥 두면 시간이 지날수록 격차가 벌어지기 마련이다. step마다 1점(실력 격차 0.2 * 인원수 5)의 차이가 벌어진다고 생각할 수 있다.

 

    그럼 여기에 더해 5번부터 7번 규칙을 적용해서 추가 팀원이라는 어드밴티지로 조율하면 어떻게 될까?

 

    먼저 양성 순환 구조형 농구에서는 잘하는 팀에 인원이 점점 추가되기에 step이 증가할수록 step마다의 격차 또한 지수적으로 증가할 것이라고 예측할 수 있다. (지수적인 이유는 5점이라는 고정된 점수마다 팀원이 추가되는데, 팀원이 추가될수록 step마다의 격차는 0.4점만큼 누적해서 증가하기 때문이다. 예를 들어, 50점 차이가 나서 팀원이 15명이 되는 순간부터는 step마다의 격차가 5점 이상이기에 step마다 팀원이 추가된다.)

 

    다음으로 부정 회귀 구조형 농구에서는 못하는 팀에 인원이 점점 추가되기에 step이 증가할수록 step마다의 격차가 줄어들어 결국 엎치락뒤치락 우열을 가릴 수 없게 된다고 예측할 수 있다.

 

    이는 발산하는 긍정형 피드백 루프와 수렴하는 부정형 피드백 루프의 구조를 반영한 것으로 책에서는 이런 예시를 통해 피드백 루프를 설명했다.

 

 

 

Machinations.io를 활용한 모델링

 

    <Game Mechanics>에서는 'Machinations.io'라는 게임 경제 시각화 툴을 소개하고, 이를 통해 결과를 확인한다. 나도 실제로 테스트해 보기 위해서 해당 툴에 접근해 봤는데, 이 과정에서 옛날 옛적에 <뚜두 농장>에 적용해 보겠다며 만들었던 걸 찾았다.

 

 

게임 경제를 시각화하는 툴

 

    'Machinations.io'는 이런 식으로 게임 경제를 노드로 정리해서 시뮬레이션을 통해 시각화할 수 있는 툴이다. 나는 이에 앞서 설명한 농구 게임을 시각화해보려고 했는데, 책에 오류가 있는 것 같아서 몇 가지 수정을 해봤다. 아래는 책에 나온 양성 순환 구조의 예시를 시각화한 케이스다.

 

 

차이가 커질수록 파란팀(A) 인원이 증가하고, 빨간팀(B) 인원은 감소한다.

 

    책에 B팀의 최소 인원은 5로 처리했다고는 하는데 B팀 인원을 굳이 빼줄 이유가 없어보였다. 이에 왜 빼주는지 이해가 되지 않아서 $-\frac{1}{5}$ 부분을 삭제했다. 이렇게 해서 아래와 같이 테스트를 진행해 봤다.

 

 

테스트 과정

양성 순환 구조 (긍정형 피드백 루프) 테스트 결과

부정 회귀 구조 (부정형 피드백 루프) 테스트 결과

 

    책에서 설명한 결과는 양성 순환 구조에서는 지수적으로 격차가 벌어지며, 부정 회귀 구조에서는 격차가 일정 값으로 안정된다고 하는데 그대로 진행됨을 확인할 수 있었다.

 

    다만, 책에서는 앞서 예상한 것과는 다르게 부정 회귀 구조에서는 엎치락뒤치락하지 않고 그저 일정한 격차를 유지한다는 점이 흥미롭다고 말하는데, 개인적으로 이런 격차가 유지되는 건 다음의 2가지 이유 때문이라고 생각한다.

 

1. 어드밴티지가 계수가 조정되지 않았다.
   
     현재는 5점 차이가 나면 1명을 투입하는 방식인데 이걸 3점, 1점과 같이 줄이다 보면 격차에 대한 기댓값이 줄어들 것이다. 그리고, 이는 확률적으로 시뮬레이션(찾아보니 몬테 카를로 시뮬레이션이라고 한다.)하면 격차가 줄어든 만큼 더 엎치락뒤치락할 것이다.
2. 실습 조건에서는 5점마다 1명이 투입되는 게 아닌 1명마다 0.2명씩 투입되기에 기댓값 계산 느낌이 섞이게 된다.
   
     위의 GIF에서 확인할 수 있듯이 팀에 인원이 추가될 때는 5점 단위로 추가되는 것이 아닌 1점 단위로 0.2명이 추가되게 된다. 따라서, 위의 테스트에서는 몬테 카를로 시뮬레이션을 진행했지만, 인원에 대해서는 기댓값을 계산했기에 이 둘이 섞여 일정한 격차를 유지한 것이라는 생각이 든다.

 

    결국 'Machinations.io'을 활용하여 실습을 하기에는 복잡하기도 하고, 나중에 협업을 할 때에도 위의 노드를 보여주며 근거를 세울 수도 없으니 부적절하다고 생각했다.

 

    이에 파이썬을 활용해서 내 입맛대로 테스트를 진행해 보기로 했다.

 

 

 

Python으로 변환 및 시각화

 

    파이썬 시각화는 군입대 전에 잠깐 머신러닝을 공부했던 경험을 살려서 'Jupyter Notebook'과 'matplotlib'를 활용해 진행했다. 그리고, 위의 실습을 변환하는 과정에서 아래와 같은 것들을 수정해 봤다.

 

1. 테스트해보기 용이하게 주요 요소들을 따로 변수로 정리했다.
2. 테스트 이전에 잘하는 팀과 못하는 팀을 따로 지정하지 않고, 그저 점수 차이가 나면 피드백 루프 의도에 맞도록 인원이 투입되게 수정했다.
3.  기댓값 계산과 몬테 카를로 시뮬레이션으로 구분하여 코드를 작성했다.

 

    코드를 그냥 막 짜서 부끄러우니 블로그에는 몬테 카를로 시뮬레이션 코드 하나만 올려두도록 하겠다..😅😅 혹시라도 직접 해보고 싶은 사람이 있다면 Github 링크를 확인 바란다.

 

# TEST 1_2 : Conducting Monte Carlo simulation

import math
import numpy as np
import matplotlib.pyplot as plt
import random

steps = 50;



# factor of Test1
numA = 5;
numB = 5;
abilityA = 0.4;
abilityB = 0.2;
advantageCriteria = 5;



# initialize positive loop result array
PLpointA = np.zeros(steps, dtype=np.int64)
PLpointB = np.zeros(steps, dtype=np.int64)
PLdifference = np.zeros(steps, dtype=np.int64)

PLpointA[0] = PLpointB[0] = PLdifference[0] = 0;
PLnumA = numA;
PLnumB = numB;

# set positive loop data
for step in range(1, steps):
    if PLpointA[step-1] > PLpointB[step-1]:
        PLnumA = numA + math.trunc(PLdifference[step-1]/advantageCriteria) if numA + math.trunc(PLdifference[step-1]/advantageCriteria) > PLnumA else PLnumA    
    else:
        PLnumB = numB + math.trunc(PLdifference[step-1]/advantageCriteria) if numB + math.trunc(PLdifference[step-1]/advantageCriteria) > PLnumB else PLnumB
    
    
    PLpointA[step] = PLpointA[step-1]
    PLpointB[step] = PLpointB[step-1]
    
    for teamMember in range(PLnumA) :
        if random.random() <= abilityA :
            PLpointA[step] += 1;
        
    for teamMember in range(PLnumB) :
        if random.random() <= abilityB :
            PLpointB[step] += 1;
    
    
    PLdifference[step] = abs(PLpointA[step]-PLpointB[step])
    
    
    
# initialize negative loop result array
NLpointA = np.zeros(steps, dtype=np.int64)
NLpointB = np.zeros(steps, dtype=np.int64)
NLdifference = np.zeros(steps, dtype=np.int64)

NLpointA[0] = NLpointB[0] = NLdifference[0] = 0;
NLnumA = numA;
NLnumB = numB;

# set positive loop data
for step in range(1, steps):
    if NLpointA[step-1] > NLpointB[step-1]:
        NLnumB = numB + math.trunc(NLdifference[step-1]/advantageCriteria) if numB + math.trunc(NLdifference[step-1]/advantageCriteria) > NLnumB else NLnumB   
    else:
        NLnumA = numA + math.trunc(NLdifference[step-1]/advantageCriteria) if numA + math.trunc(NLdifference[step-1]/advantageCriteria) > NLnumA else NLnumA
  
    
    NLpointA[step] = NLpointA[step-1]
    NLpointB[step] = NLpointB[step-1]
    
    for teamMember in range(NLnumA) :
        if random.random() <= abilityA :
            NLpointA[step] += 1;
        
    for teamMember in range(NLnumB) :
        if random.random() <= abilityB :
            NLpointB[step] += 1;
    
    NLdifference[step] = abs(NLpointA[step]-NLpointB[step])

    

x = np.arange(0, steps, 1)

plt.plot(x, PLpointA, color="Blue")
plt.plot(x, PLpointB, color="Red")
plt.plot(x, PLdifference, color="Black", linestyle="--")
plt.grid()
plt.show()

plt.plot(x, NLpointA, color="Blue")
plt.plot(x, NLpointB, color="Red")
plt.plot(x, NLdifference, color="Black", linestyle="--")
plt.grid()
plt.show()

 

 

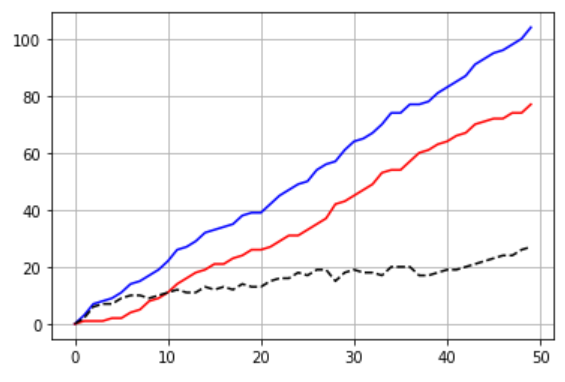
    이렇게 파이썬으로 테스트한 결과는 다음과 같다. 가로축은 step, 세로축은 점수를 가리키며, 파란색과 빨간색 실선은 각 팀의 점수를, 검은색 점선은 각 팀의 점수 차를 가리킨다.

 

 

(좌) 기댓값 계산 결과, (우) 몬테 카를로 시뮬레이션 결과

 

    결과는 예상과 같이 동작하며, 앞서 아래와 같이 'Machinations.io'에서 테스트한 결과 동일한 추세를 보인다는 걸 확인할 수 있다.

 

 

(좌) 양성 순환 구조, (우) 부정 회귀 구조

 

    위에서 확인한 것처럼 기댓값 계산과 몬테 카를로 시뮬레이션을 분리한 것을 통해 이론적으로 어떤 경향성을 보일지와 실제로 어떤 식으로 동작할지를 비교 확인할 수 있었다.

 

    잠깐 확인해 보면 양성 순환 구조의 기댓값 계산에서는 우리의 예상과 같이 점수 차이가 지수적으로 발산하는 걸 확인할 수 있었으며, 부정 회귀 구조에서는 'Machinations.io'에서 확인한 것보다 더 정확하게 일정 step 이후부터는 동일한 간격을 유지하며 점수 차이가 수렴하는 걸 확인할 수 있었다.

 

 

 

가설과 검증

 

    그럼 이제 이렇게 만든 환경으로 가설을 세워보고, 이를 확인하며 괴리를 줄여나가보도록 하자.

 

 

  # 부정 회귀 구조에서 어드밴티지 계수가 조정하여 더 치열한 양상을 유도할 수 있을 것이다.

 

    기댓값 계산에서는 일정한 점수 격차를 보인다고 해도, 몬테 카를로 시뮬레이션에서는 확률에 의해 노이즈가 더해지게 된다. 이에 경기가 엎치락뒤치락되도록 유도하기 위해서는 노이즈의 영향력을 키워야 하고, 이를 위해서 다음의 2가지 방식으로 접근할 수 있을 것이다.

 

1. 점수 격차의 기댓값을 줄인다. (어드밴티지를 더 크게 만든다.)
2. 노이즈의 크기를 키운다. (확률적인 요소가 갖는 영향력을 강화한다.)

 

    먼저 첫 번째 방법부터 확인해 보자. 현재 실험 환경의 어드밴티지는 팀원을 투입하는 방식으로 제공되며, $\frac{\|difference\|}{5}$라는 공식에 의해 만들어진다. 그리고, 여기에서 5는 어드밴티지가 얼마나 큰 차이마다 제공될 것인지를 의미한다.

 

    첫 번째 방법에서는 점수 격차의 기댓값을 줄이기로 했으니 어드밴티지가 더 자주 제공되도록 하기 위해 이 값을 줄여보자. 다음은 위 코드에서 advantageCriteria(어드밴티지 기준을 가리키는 변수)을 각각 5, 3, 1로 했을 때의 기댓값 계산과 몬테 카를로 시뮬레이션 결과다.

 

 

기댓값 계산 결과 : 순서대로 5, 3, 1

몬테 카를로 시뮬레이션 결과 : 순서대로 5, 3, 1

 

    한눈에 봐도 어드밴티지의 영향력이 클수록 더 자주 엎치락뒤치락하는 걸 확인할 수 있다.

 

 

    다음으로 두 번째 방법은 노이즈의 크기를 키우는 것이다. 처음에는 단순히 실력에 대한 확률(점수를 얻을 확률)을 제곱해서 확률에 대한 영향력을 키우려고 했다. 실제로 각각 0.5를 제곱하니 그럴 듯 해보이는 결과가 나오기도 했고 말이다.

 

    그러나, 확률을 제곱한 게 어떤 영향을 끼치는지 확인해 보니 노이즈를 키운다기보다는 실력 격차에 따른 영향을 조정하는 것이라는 걸 알 수 있었다. 아래의 그래프를 살펴보자.

 

 

(좌) 제곱 시 지수에 따른 값 변화, (우) 제곱 시 비율 변화

 

    그래프에서 확인해 보면 지수가 1일 때는 실력 격차가 2배였는데, 지수 값에 따라 그 비율이 달라진다는 것, 그렇기에 실력을 제곱하는 건 확률에 따른 노이즈를 키우는 것이 아닌 실력 격차에 따른 영향을 조정하는 것이라는 것을 알 수 있다.

 

    그래서, 단순하게 확률에 따른 노이즈를 키우기 위한 방법으로 가장 간단하게 득점 시 얻을 수 있는 점수를 증가시켰다. 아래는 득점 시 3점을 얻을 수 있을 때의 몬테 카를로 시뮬레이션 결과다.

 

 

득점 시 3점을 얻을 수 있을 때의 결과

 

    결과를 보면 더욱 치열해진 것을 확인할 수 있다. 다만, 여기서 노이즈가 심해진 것 같지 않아서 10점을 얻을 수 있게도 해봤는데 다음과 같은 완만한 결과를 얻을 수 있었다. 

 

 

(좌) 완만하다, (우) 24.09.08 - 그래프를 확장해서 확인한 모습 : 예상대로 나름 격하게 우열이 나뉜다.

 

 

    5점 차이 이상 벌어진 경우 바로 어드밴티지가 주어져서 그런가 완만하다. 다만, 1점이 주어질 때에 비해 확실히 치열해졌기에 유의미하다고 판단하여 이렇게 정리해 봤다.

 

    내 예상으로는 뾰족뾰족한 형태로 치열할 줄 알았는데 생각보다 완만하게 치열해서 예상외였다. 이 부분에 대해서는 조금 더 알아봐야 될 것 같다. 아마 오늘처럼 계속 수치를 가지고 이것저것 하다 보면 자연스레 알게 되지 않을까..? (라는 핑계를 대봅니다.. 😂😂)

+ 24.09.08 추가)
  완만한 이유는 실제로 완만해서가 아닌 y 척도가 달라져서 그렇다. 이전 그래프에서는 400까지 올라가는데 반해, 득점 시 10점을 얻게 하는 경우에는 총 득점이 5000까지 크게 올라가는 걸 확인할 수 있다.

 

 

    가설과 검증이라는 항목을 두고 하나만 작성하는 게 조금 걸리긴 하는데, 슬슬 피곤해져서 오늘은 이쯤하고 마무리 짓겠다.

 

 

 

결론

 

1. 양성 순환 구조의 플레이에서는 팀 간 격차가 발산한다.
2. 부정 회귀 구조의 플레이에서는 팀 간 격차가 특정 값에 수렴한다.
3. 어드빈티지의 강도와 빈도를 조절하여 더 치열한 양상을 유도할 수 있다.
4. 플레이어의 퍼포먼스 중 운이 차지하는 비중을 높여 더 치열한 양상을 유도할 수 있다.

 

 

 

마치며

 

    오늘은 밸런싱 관련 인사이트를 얻기 위한 환경을 마련하고, 간단하게 한 가지 가설에 대한 검증을 진행해 봤다. 사실 위에서 정리한 결론들은 굳이 이렇게까지 하지 않더라도 금방 찾고 이해할 수 있는 인사이트들이라 이렇게 정리한 게 부끄럽긴 하다.

 

    그러나, 내가 생각하기에 이런 사소한 인사이트부터 직접 확인하고 검증해 보는 경험이 추후 나만의 인사이트를 찾았을 때 이를 실제로 활용하고 발전시킬 수 있도록 호응할 것이라고 생각하기에 이렇게 진행해 봤다.

 

    추가로, 이런 수치 분석과 튜닝을 통해 수치와 의미를 연결 지어 가지고 놀 수 있는 어떤 능력을 키울 수도 있을 것 같기도 하고 말이다. 

 

 

    아무튼 이번에 처음으로 밸런싱 관련해서 무언가를 해보고 정리해 봤는데, 처음이라 그런지 생각처럼 잘 안 되고, 시간도 꽤 오래 걸린 것 같다. 원래 처음이 복잡하고 어려운 법이니 차차 나아질 거라고 생각한다. 이를 통해 최종적으로는 증명할 수 있는 튜닝을 할 수 있기를 바란다.

 

    그럼 오늘의 글은 이쯤하고 여기서 마치도록 하겠다. 아직 위의 환경에서 테스트해볼 수 있는 게 많이 남아있는 것 같아서 조만간 시간 날 때 다시 한번 해당 주제로 찾아오도록 하겠다.

 

    아래에 간단하게 이후에 할 것들을 정리하며 마무리 짓겠다. 긴 글 읽어줘서 고맙고, 오늘도 좋은 하루 보내길 바란다.

 

1. 밸런싱 요소(factor)를 다른 수식에 적용할 수 있게 일반화하여 이해해 보는 것.
2. 수치가 특정 영역 내에서 활동하도록 제어하는 방법을 찾아보는 것.
3. 점화식 형태의 수식을 일반항으로 정리하여 밸런싱해 보는 것.
4. RPG에서 몬스터 사냥 시의 역치를 분석해 보는 것.

 

 

 

오늘의 선곡!